Near and far-field diffraction

We will demonstrate the near and far-field propagators in HCIPy. We’ll use both a circular aperture and the LUVOIR-A telescope pupil as example pupils.

We first start by importing the relevant python modules.

from hcipy import *

import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

To make life simpler later on, we define a function to nicely show two fields side-to-side, with a nice spacing, titles and axes labels.

def double_plot(a, b, title='', xlabel='', ylabel='', **kwargs):
    '''A function to nicely show two fields side-to-side.
    '''
    fig, axes = plt.subplots(1, 2, gridspec_kw={'left': 0.14, 'right': 0.98, 'top': 0.95, 'bottom': 0.07, 'wspace': 0.02})
    fig.suptitle(title)

    imshow_field(a, **kwargs, ax=axes[0])
    imshow_field(b, **kwargs, ax=axes[1])

    axes[1].yaxis.set_ticks([])
    axes[0].set_xlabel(xlabel)
    axes[1].set_xlabel(xlabel)
    axes[0].set_ylabel(ylabel)

    return fig

Now we can create the pupils. Each pupil will have the same diameter of 3mm, and we’ll use a wavelength of 500nm. Each pupil is evaluated with supersampling, meaning that the value at each pixel will be the average of, in our case, 8x8=64 subpixels. We’ll use 256 pixels across and enlarge the pupil plane slightly to be able to see the details in the near-field diffraction just outside of the pupil.

pupil_diameter = 3e-3 # meter
wavelength = 500e-9 # meter

pupil_grid = make_pupil_grid(256, 1.2 * pupil_diameter)
aperture_circ = evaluate_supersampled(circular_aperture(pupil_diameter), pupil_grid, 8)

aperture_luvoir = evaluate_supersampled(make_luvoir_a_aperture(True), pupil_grid.scaled(1 / pupil_diameter), 8)
aperture_luvoir.grid = pupil_grid

wf_circ = Wavefront(aperture_circ, wavelength)
wf_luvoir = Wavefront(aperture_luvoir, wavelength)

And plotting both apertures next to each other:

double_plot(aperture_circ, aperture_luvoir,
            xlabel='x [mm]', ylabel='y [mm]',
            grid_units=1e-3, cmap='gray')
plt.show()
../../_images/output_7_0.png

Near-field propagation

Near-field diffraction is used for propagation of waves in the near field. In HCIPy we have currently two propagators for simulating near-field diffraction. We will only use the :class:FresnelPropagator. This propagator uses the paraxial Fresnel approximation to propagate a :class:Wavefront. We can create the propagator as follows:

propagation_distance = 0.1 # meter

fresnel = FresnelPropagator(pupil_grid, propagation_distance)

Afterwards we can simply propagate a wavefront through the created Fresnel propagator by calling it with the wavefront. Alternatively, you can also call the propagator.forward() or propagator.backward() functions for forward and backward propagation.

img_circ = fresnel(wf_circ)
img_luvoir = fresnel(wf_luvoir)

And plotting the result.

double_plot(img_circ.intensity, img_luvoir.intensity,
            xlabel='x [mm]', ylabel='y [mm]',
            vmax=2, cmap='inferno', grid_units=1e-3)
plt.show()
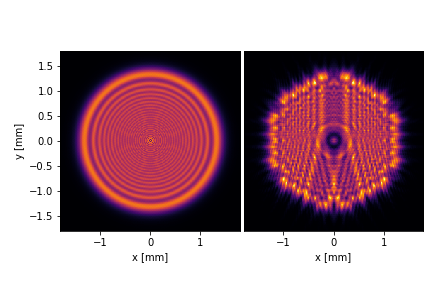
../../_images/output_13_0.png

We can modify the distance by changing the distance parameter of the propagator. Alternatively, we can create a new :class:FresnelPropagator object using the new distance.

fresnel.distance = 1 # meter

img_circ = fresnel(wf_circ)
img_luvoir = fresnel(wf_luvoir)

double_plot(img_circ.intensity, img_luvoir.intensity,
            xlabel='x [mm]', ylabel='y [mm]',
            vmax=2, cmap='inferno', grid_units=1e-3)
plt.show()
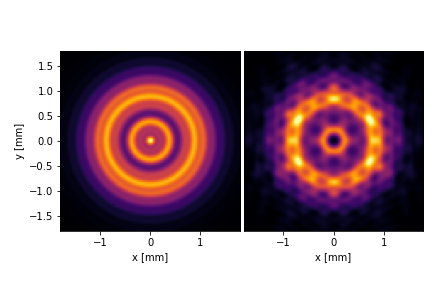
../../_images/output_15_01.png

It’s always nice to see the full transition from near-field to far-field diffraction. We’ll make an animation to slowly transition from 0 to 20 meters.

def easing(start, end, n):
    x = np.linspace(0, 1, n)
    y = np.where(x < 0.5, 4 * x**3, 1 - 4 * (1 - x)**3)

    return y * (end - start) + start

# Setting up the propagation distances in the animation
n = 35
propagation_distances = np.concatenate([easing(0, 0.1, n),
                                        easing(0.1, 1, n),
                                        easing(1, 5, n),
                                        easing(5, 20, n),
                                        easing(20, 0, 2 * n)])

# Starting the animation object to write to an mp4 file.
anim = FFMpegWriter('near_field.mp4', framerate=11)

for propagation_distance in propagation_distances:
    # Set the propagation distance
    fresnel.distance = propagation_distance

    # Propagate both wavefronts
    img_circ = fresnel(wf_circ)
    img_luvoir = fresnel(wf_luvoir)

    # Plotting the current frame of the animation.
    double_plot(img_circ.intensity, img_luvoir.intensity,
                title='Distance: %.3f meter' % propagation_distance,
                xlabel='x [mm]', ylabel='y [mm]',
                vmax=2, cmap='inferno', grid_units=1e-3)

    # Adding the frame to the mp4 file and closing the created figure.
    anim.add_frame()
    plt.close()

anim.close()

anim

Far-field propagation

Far-field diffraction uses the Fraunhofer approximation to propagate waves. In high-contrast imaging, we often use lenses or mirrors with a specified focal length to focus the light from a pupil plane into a focal plane. In HCIPy we can do the same thing with a :class:FraunhoferPropagator object. This propagator propagates from a pupil to a focal plane with a perfect lens.

First we have to define our focal length and the sampling of the focal plane that we want to get out.

focal_length = 0.5 # meter

spatial_resolution = focal_length / pupil_diameter * wavelength
focal_grid = make_focal_grid(8, 12, spatial_resolution=spatial_resolution)

Then we can create our :class:FraunhoferPropagator object and pass the pupil and focal grids, and the focal length of its perfect lens.

fraunhofer = FraunhoferPropagator(pupil_grid, focal_grid, focal_length=focal_length)

Then we can propagate our wavefronts and plot the resulting images as usual.

img_circ = fraunhofer(wf_circ)
img_luvoir = fraunhofer(wf_luvoir)

double_plot(img_circ.power, img_luvoir.power,
            xlabel='x [um]', ylabel='y [um]',
            cmap='inferno', grid_units=1e-6)
plt.show()
../../_images/output_23_0.png

Due to the contrast in the focal plane, there is barely any difference between the two telescope pupils. We can make this clearer by showing the images on a logarithmic scale.

double_plot(np.log10(img_circ.power / img_circ.power.max()), np.log10(img_luvoir.power / img_luvoir.power.max()),
            xlabel='x [um]', ylabel='y [um]',
            vmin=-6, cmap='inferno', grid_units=1e-6)
plt.show()
../../_images/output_25_01.png

Changing the focal length is as simple as modifying the focal_length parameter, or we can create a new propagator with the new focal length. The PSF shrinks with a smaller focal length of 30cm.

fraunhofer.focal_length = 0.3 # m

img_circ = fraunhofer(wf_circ)
img_luvoir = fraunhofer(wf_luvoir)

double_plot(np.log10(img_circ.power / img_circ.power.max()), np.log10(img_luvoir.power / img_luvoir.power.max()),
            xlabel='x [um]', ylabel='y [um]',
            vmin=-6, cmap='inferno', grid_units=1e-6)
plt.show()
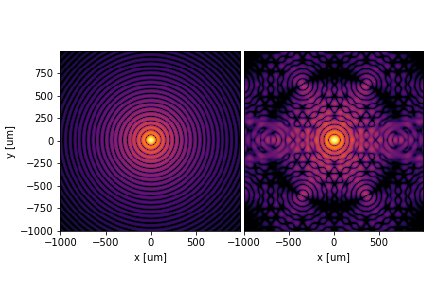
../../_images/output_27_0.png

Changing the wavelength is done by changing wavelength parameter of the :class:Wavefront objects that are passed to the propagators. With a smaller wavelength of 350nm, our PSFs will shrink even more.

wf_circ.wavelength = 350e-9 # meter
wf_luvoir.wavelength = 350e-9 # meter

img_circ = fraunhofer(wf_circ)
img_luvoir = fraunhofer(wf_luvoir)

double_plot(np.log10(img_circ.power / img_circ.power.max()), np.log10(img_luvoir.power / img_luvoir.power.max()),
            xlabel='x [um]', ylabel='y [um]',
            vmin=-6, cmap='inferno', grid_units=1e-6)
plt.show()
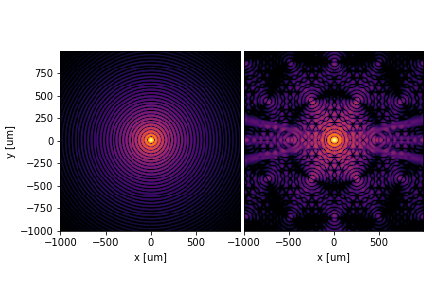
../../_images/output_29_0.png

Of course, we can easily create an animation of the PSF changes with wavelength.

fraunhofer.focal_length = 0.5 # meter

n = 50
wavelength_max = 700e-9
wavelength_min = 350e-9

wavelengths = np.concatenate([easing(wavelength_min, wavelength_max, n),
                              easing(wavelength_max, wavelength_min, n)])

anim = FFMpegWriter('far_field.mp4', framerate=15)

for wl in wavelengths:
    wf_circ.wavelength = wl
    wf_luvoir.wavelength = wl

    img_circ = fraunhofer(wf_circ)
    img_luvoir = fraunhofer(wf_luvoir)

    double_plot(np.log10(img_circ.power / img_circ.power.max()), np.log10(img_luvoir.power / img_luvoir.power.max()),
                title='Wavelength: %d nm' % (wl * 1e9),
                xlabel='x [um]', ylabel='y [um]',
                vmin=-6, cmap='inferno', grid_units=1e-6)

    anim.add_frame()
    plt.close()

anim.close()

anim

# Cleanup created files
import os

os.remove('near_field.mp4')
os.remove('far_field.mp4')